Ask Miss Science

How To Make A Shih-Tzu Float

Dear Miss Science: Given a 16.5-lb. Shih-Tzu which breaks down to approximately 14.5 lbs. of dog and 2 lbs. hair, how many standard-size mylar balloons filled with helium would I have to tie to him to achieve gravitational lift-off, and how many would I have to use to achieve an aerial height of at least eighteen inches?

-- Helly (actually posting for Finnovar the cat, because of course I would never need to know such a thing)

Finnovar the Huge in his natural habitat:


Though this question seems relatively simple, the answer -- or, rather, its associated explanation -- is a bit lengthy. I opted for length so that I could explain how I arrived at the answer in some detail. However, I understand that there are those who will not be interested in the details. To help readers find the details that most interest them I have divided the answer into appropriate sections. The reader is encouraged to skim through and read only those portions of interest.

I would also like to thank Helly and Dad for proofreading an early version of this!

The Answer (vague though it may be)

I cannot give you a number that will work in all cases.  Neither can I tell you how to achieve the 18-inch hover without knowing very specific information about the particular air in which your dog will be floating.

However, I can give you an approximate number of balloons required simply for lift-off assuming that your air is at about 77° F and that the air pressure is 1 atmosphere. That answer is somewhere between one thousand and two thousand, depending on the nature of the balloons being used.  I got that number range from calculations based on measurements of the masses and volumes of two balloons I purchased.

Basic Principles

The calculation itself contains quite a few steps, but the basic principle isn't very hard to understand. In short, the combination of dog and balloons must be lighter than (weigh less than) the air that would otherwise be present (Figure 1).

Figure 1


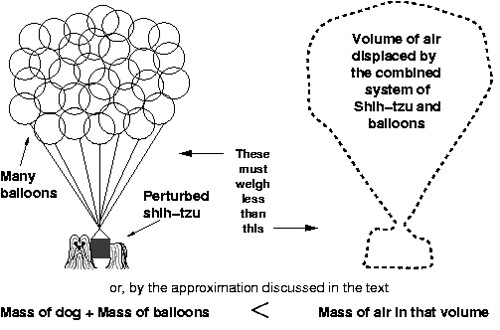
Put another way, the density of the dog and balloon system must be less than or equal to the density of the air surrounding them (recall that density is mass divided by volume).

Note that by using density I am using mass where, technically, I should use weight. However, for this problem the difference is trivial and mass makes the calculation simpler. The curious reader should see Note 1 for more information.

Here is the density sentence (just above, starts with "Put") written as an equation:

Density of air >= Density of dog and balloons     [Equation 1]

If the density of the dog and balloon system is lower than the surrounding air, the dog and balloon system will rise.  Since, typically, air becomes less dense as one rises, the dog and balloon system will continue to rise until a point where their density is the same as the surrounding air. 

In order to predict the number of balloons needed to achieve the 18-inch hover, you would need to know, in some detail, how the density of the air around the dog and balloons varies with height.  A far simpler approach would be to add and subtract balloons in-situ until the desired height is achieved.

However, before you start, it's a good idea to estimate the required number of balloons.  Based on my first calculation, you would need about 1400 balloons, give or take 250.  But, when I tried a second balloon, I calculated a slightly larger number. Given the differences between the two measurements, it might be safer just to say that you will need between one thousand and two thousand balloons. See the measurements section for more information about the two balloons I used.

Calculation Details:

Readers who already know how to perform this calculation might want to skip this section. It was written for readers who do not engage in these sorts of calculations regularly, and the calculations are explained in great detail. Readers who are not so experienced and wish to gain understanding of this sort of calculation are especially encouraged to read this section. If you are in this category, it might help to follow along with pen and paper, writing down the equations and notes regarding their meaning. Skip to the measurements section.

In this section, I'll explain how I got the base number of balloons (1400) for the first balloon. The calculation would be the same for any other balloon, but using the mass and volume of that balloon. At the end, I'll explain very briefly how I decided on the 1000-2000 range.

We'll start with Equation 1:

Density of air >= Density of dog and balloons     [Equation 1]

To make the math easier, let's only be concerned with the case where the two densities are equal. Doing this gives us the minimum number of balloons we need -- then we can add more balloons until the dog rises to the desired height.  So, I'll rewrite the equation:

Density of air = Density of dog and balloons     [Equation 2]

To find the number of balloons, we need to modify this equation so that it contains a number of balloons.  Once we've done that, we'll need to do a little algebra.  Then we'll have our number. 

Since the right side of the equation concerns the balloons, we should start by taking a closer look there. It's usually best to start by examining the definitions of any terms. We'll get to "dog" and "balloon" shortly. For now, though, let's define density.

Density is mass divided by volume.  As translated into mathematical notation, that is:

D = M / V      [Equation 3]

where D is density, M is mass and V is volume.

Now we need to apply Equation 3 to our situation.  Here, the density of our system is the mass of the whole system over the volume of the system.  In other words, we need to add up all the masses (dog, balloons, hair, harness, hair, string, hair, etc.) and divide that combined mass by the volume taken up by all those items.  Written mathematically, that is:

D_{dog and balloons} = (M_dog + M_{all balloons})  /  (V_dog + V_{all balloons})   [Equation 4]

In Equation 4, M_dog and V_dog refer to all dog-related masses and volumes (dog, hair, harness, collar, etc.), and M_{all balloons} and V_{all balloons} refer to the combined masses and volumes of all balloon-related items (string, mylar, helium, etc.). 

We can easily work a number of balloons into the right side of Equation 4 by assuming that the total mass of all the balloons can be determined, approximately, by multiplying the mass of one balloon by the number of balloons.  The volume of the balloons can be determined similarly.   (This assumption, of course, is a source of error in our calculation, but at least it gives us an answer.)  Now, we can say:

D_{dog and balloons} = (M_dog + N*M_balloon)  /  (V_dog + N*V_balloon)    [Equation 5]

Here N is the number of balloons, M_balloon is the mass of one balloon, and V_balloon is the volume of one balloon.  N is the number we want.  If we substitute the right side of Equation 5 for the right side of Equation 2, we get:

D_air =  (M_dog + N*M_balloon)  /  (V_dog + N*V_balloon)    [Equation 6]

Here, "D_air" = "Density of air" (for brevity).  After a little algebra, we get the result in Equation 7, below.  It is left as an exercise to the curious reader to check my algebra.

N = (M_dog - V_dog*D_air) / (V_balloon*D_air - M_balloon)   [Equation 7]

Now, we need to see if we have all the numbers we need.  If we don't, then we need to find some way to get them.  The question only supplied one number, the mass of the dog (M_dog).  We also need the volume of the dog (V_dog), the density of the air (D_air), and the mass and volume of a balloon (M_balloon and V_balloon). 

Truth be told, the volume of the dog can be ignored, but it would take a paragraph or two to explain why, so I'll leave it in.  I estimated that the volume of a shih tzu is about 10 liters, give or take 5.  That's a pretty reasonable estimate.  An average shoebox is about 5 liters, so 10 might even be a bit high, but it won't make much difference to the final answer.  So, we have a number:   V_dog = 10 L.

The density of air is available from a number of sources. I calculated the density of air at 1 atm pressure and a temperature of about 77 °F using information in this document (pdf file) concerning the composition of air. The density I calculated is 1.184 grams per liter. I'll spare you the details of how I calculated the density here. Feel free to ask, though, if you want to know.

I measured and/or calculated the other values.  Detailed descriptions of these procedures can be found below, but I'll give the answers here.  I measured the mass of the empty balloon-skin and its string as  11.13 g, and I calculated the mass of the helium in the balloon to be 2.65 g.  The combination of these masses gives M_balloon = 13.78 g.  I measured the volume of the filled balloon and found V_{filled-balloon}= 16.2 liters. 

I also converted the weight of the dog in pounds to mass in grams.  The mass in grams is 7484.2.

Now, we know all of the numbers we need and can substitute them in to Equation 7:

N = ( (7484.2 g) - (10 L)*(1.184 g/L) ) / ( (16.2 L)*(1.184 g/L) - (13.78 g) )   [Equation 7, substituted]

or,

N = 1383.57

Assuming we won't have any partial balloons, at least 1384 balloons will be needed.  However, considering my assumptions about the dog volume and the lack of data concerning the consistency of grocery-store balloons, it seems more reasonable to simply say that around 1400 balloons will be needed.  Once I figured in the error sources known to me, I found that the number might actually be somewhere between about 1150 and 1650.  I will spare you the details of this calculation, but I got the range by performing the calculation two more times, once assuming all the errors made the number as high as possible and again assuming all the errors made the number as low as possible.  After considering the second balloon (see below) and all the error sources not known to me, I decided it would be safest to say the number is somewhere between one thousand and two thousand.

Note that these numbers, as vague as they are, are only true for air at 1 atm and 77 °F. If your air is hotter or colder or a high- or low-pressure system is in the area, the numbers will change.

Other Measurements and Calculations:

Top. Basic Principles. Calculations.

In this section I describe how I measured the volumes and masses of the balloons and, briefly, how I calculated the mass of helium in the balloons.

General Notes Regarding the Measurements:

I looked around on the internet, but was unable to find any information on mass or volume of mylar balloons (except for one technical paper -- see Note 2).  So, I bought a balloon.  The first balloon I purchased wasn't mylar -- rather, it was a thin, non-elastic plastic without the metallic luster of mylar.  After deciding that I should answer the question as asked, I also bought a mylar balloon.   In both cases, I picked the most common size available at the large-chain grocery store from which I purchased the balloon.  Each cost $2.99 plus tax.  Although mylar is actually a form of plastic, I will use the term "mylar" to refer to the mylar balloon and "plastic" to refer to the other.

One should note that the procedures outlined below would not be acceptable for traditional, elastic balloons.  Since mylar and similar balloons are not elastic -- that is, they will not significantly compress the helium inside them -- the simple procedures outlined below are sufficient.

Measuring the Balloons' Volumes:

First, I measured the volumes of the filled balloons.  To do this, I filled a 10-gallon plastic storage bin completely full of water.  Since the mylar balloon had deflated slightly (I keep my house a bit cold), I used hot water for the mylar balloon so that the heat from the water would cause the balloon to fully expand.  After filling the bin with water, I pushed the balloon just barely under the surface making sure to keep as much of the balloon and as little of my fingers, as was possible, under water.  It was difficult to maintain a perfect balance, which will certainly introduce error into the measurement.  However, gauging the sizes of my fingertips and the small amount of balloon I left sticking out, I'd say the error will be on the order of a few milliliters (one-thousandth of a liter) and maybe less.   Pushing the balloon under water, of course, caused water to flow out of the bin.  I held the balloon still until water stopped flowing out of the bin.  Then, I removed the balloon and shook it so that most of the water on it would go back into the bin.

According to the principle usually associated with Archimedes (remember the "eureka!" story about the bathtub, the naked guy and the king's crown? -- I used the same idea here), the volume of water displaced from the bin is equal to the volume of the balloon.  To find that volume, I used a 1.50 liter bottle marked in 0.25 liter increments to refill the bin.  I kept up with the number of 1.50 liter amounts needed to refill the bin, which gave me the volume of the balloon.  The total volume I measured for the plastic balloon is 16.2 L and for the mylar balloon, 15.3 liters.  I estimate the error to be about 0.5 L and probably less.  See below in Note 2 for additional, somewhat technical discussion of this.

As an interesting side note, the small amount of water that would not shake from the balloon was enough to keep the balloon from floating.  Once I fully dried the balloon, it floated again just fine. 

As another interesting side note, since the plastic balloon appears to have been slightly larger (again, see Note 2), it would be more cost-effective to use the plastic balloon.

Measuring the Balloons' Masses:

Next, I needed to measure the mass of the balloon skin and string.  I couldn't measure the mass of the filled balloon because it would not have lain on the balance pan.  So, I punctured the balloon and massed it on an analytical balance (a very accurate and precise scale) where I teach.  Actually, I measured the mass on several balances and took the average value.   I left the string attached since, presumably, the string will be used to attach the balloon to the dog.  Using less string -- or a lighter string -- will somewhat lower the number of balloons that are required -- I measure the no-string mass, too, just to see if it would be different.

To get the mass of the helium in the balloon, I used the ideal gas law, PV=nRT.   This law allows us to calculate the number of atoms of a gas (n -- this is actually number of moles of gas, but the idea is similar) that are present at a certain pressure (P), temperature (T) and volume (V). The number of (moles of) atoms can easily be converted into a mass using the molar mass for helium. Helium's molar mass is the number just under the "He" on most periodic tables.

Notes:

Note 1: Weight is, technically, more appropriate than mass because weight includes the effect of gravity. If the somewhat significant gravitational field of the Earth were not present, this question would be rendered quite meaningless. However, since the size of the shih tzu and balloons system is very small compared to the diameter of the Earth, it is not important to account for variations in the effects of gravity. If, however, we were discussing a shih tzu, for example, tethered via a lengthy cable to a satellite, then we might do well to use weight instead of mass. This, of course, would also complicate the mathematics considerably. Back to reference in text.

Note 2: As an aside, I found, on the internet, the text of a paper published in the Journal of Nonlinear Mathematical Physics (Volume 11 Supplement, pp. 55-65, 2004).  The paper treats the geometry of a mylar balloon using elliptical integrals and reports that the volume of a mylar balloon with a deflated diameter of 9 inches to be 15.18 L.  Since I still had the mylar balloon around, I measured its deflated diameter and found it to be 9 inches.  The excellent agreement between these results indicates that my volume measurements were pretty good.  Unfortunately, I no longer had the other balloon available.  If its diameter were only slightly larger, say 9.25", then the volume would have been about 16.2 L.  My measurements will necessarily be larger than the calculations for two reasons.  One, I was unable to shake off all of the water clinging to the balloons.  Two, each balloon contains a small additional volume at the base where the balloon is filled. But, neither of these amounts constitutes more than a few dozen milliliters. The largest discrepancy is most likely due to inaccuracies in the equipment I used. Back to first reference to Note 2.

posted by Ask Miss Science @ 4:55 PM